参考
http://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91#.E6.8F.92.E5.85.A5
1.有二叉平衡树，why红黑树。
二叉平衡树的缺点，在删除时，需要调整整棵树，费时间。红黑树只需要调整局部
2.红黑树性质：
1）.所有节点非红即黑
2）.根是黑的
3）.所有叶子是黑的。（叶子指不存数据的NULL结点）
4）.红结点的儿子一定是黑的
5）.从任意结点出发，到其所有叶子节点的路径上黑色节点数相同。（同一结点到不同叶子结点路径上）
3.红黑树的插入
新插入的结点默认为红色，这样可以保证性质5），若性质4）收到威胁，再采取措施
先分析：我们可以得到
性质1）3）可以始终保持，
性质4）在增加红色结点、重绘黑色结点为红色、做旋转时受到威胁
性质5）在增加黑色结点、重绘红色结点为黑色、做旋转时受到威胁
在如下描述中，新插入的标记为N,N的父亲标记为P，N的祖父标记为G，N的叔父标记为U.先分析插入的情况
（3.1）N为根节点。直接重绘为黑色
（3.2）P为黑色。直接插入
一下情况P为红色，由1）得知，N一定有叔父结点。ps 不存数据的NULL叶子节点也可以使叔父结点。
（3.3）P和U都是红色，N为P的左儿子或右儿子。则把PU重绘黑，G重绘红。在把G当做N进行从（3.1）开始的各种情况的检查。
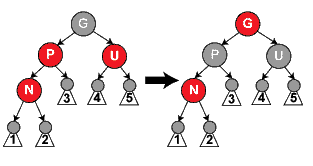
（3.4）P红色，而U为黑色（包括U为存数据的黑色以及叶子节点的黑色），N是P的右儿子，P是G的左儿子。则进行左旋，接着按（3.5）做处理
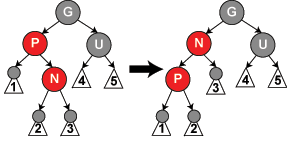
（3.5）P红色，而U为黑色（包括U为存数据的黑色以及叶子节点的黑色），N是P的左儿子，P是G的左儿子。对G进行右旋
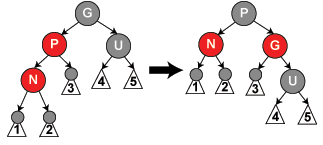
插入实际上是原地算法，上述都采用了尾部递归。
4.红黑树的删除
首先把删除两个具有两个儿子节点（非叶子儿子）的问题转化为删除另一个只有一个儿子节点的问题（非叶子儿子）。先找到左子树中最大元素或者右子树中最小元素来顶替节点，即把找到的结点先转移到要删除的结点中，接着再删除我们从中复制出的那个结点。
若选择复制左子树的最大节点，复制出的那个结点有下图三种情况（最大节点，故要删除的结点没有右儿子）。
（1）红色结点，左右儿子为不存数据的NULL。则直接删除，结束。不破坏性质
（2）黑色结点，左右儿子为不存数据的NULL。这个情况删除略微麻烦，见下面详细讨论
（3）黑色结点，左儿子为红色，右儿子为NULL。这种情况，删掉黑色后，原本指向黑色结点的指针指向黑色结点的左儿子，并把左儿子重绘为黑色，结束。
其他情况若有左儿子，则不满足性质（4），即红色结点左儿子为红色。或者性质（5），黑色结点左儿子为黑色。
下面都来讨论删除该复制出的那个结点,要删除的结点是N。删除上面第（2）中情况
（4.1）N是新根，直接删除
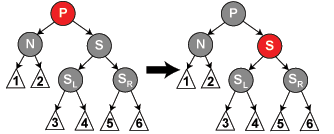
（4.2）S红色（推出P为黑）。则在P上左旋转，然后对调N的P和G的颜色。此时N的新S为黑，P为红，以左边框内作为单位，转到（4.4）（4.5）（4.6）来处理
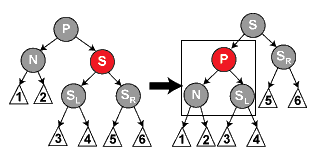
（4.3）N的P、S以及S的SL、SR都是黑色。把S重绘为红色。则该小单元在删除N后黑色个数相同，则把框内看成整体，从（4.1）开始调整。即从（4.1）开始，在P上做重新平衡处理
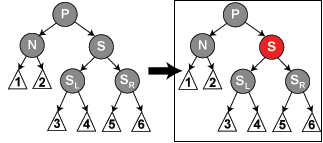
（4.4）N的P为红色，S以及SL、SR都是黑色。则把P和S的颜色交换，就完成了
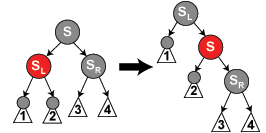
（4.5）S黑色，SL红色，SR黑色。将S做右旋，再交换SL和S的颜色，再由（4.6）处理
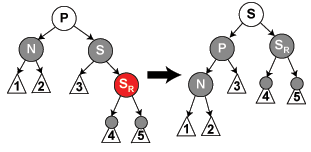
（4.6）S黑色，SR红色。在P点做左旋；交换P，S的颜色；把SR重绘为黑色。这样通过N的路径上多了一个黑色，N可以删除了
评论 (0)
