1.《剑指offer》 44页 替换空格。题目:给一个字符串"we are young",把其中空格替换为"%20".即变为"we%20are%20young"
key:先遍历字符串,统计空格数目,然后从后往前替换。在原空间上把空间加大。
2.《剑指offer》 51页 从尾到头打印链表。
思路一:顺序遍历一遍,并把结点压入栈中,然后从栈中pop出结点
思路二:递归,每访问一个结点,先递归输出其后面的结点,再输出自身的结点。
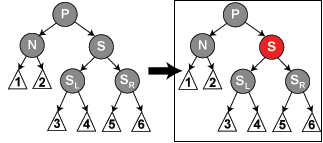
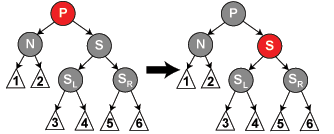
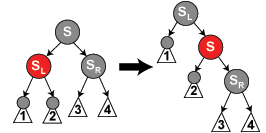
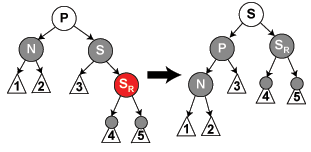
3.《剑指offer》55页,由先序遍历和中序遍历构建二叉树。
key 先序遍历第一个为根。找到根后可以再中序遍历中找到根的左子树和右子树。左右子树再利用相同的思想,于是关键就是递归了。
4.《剑指offer》59页。利用两个栈实现一个队列。
key 插入则放入stack1中,删除,则从stack2中删除。其中stack2中的元素是从stack1中pop后在push到stack2中的。
5,《剑指offer》65页。实现O(n)时间复杂度的排序算法。
key 问清楚排序数字的范围,数据的多少。然后具体问题具体分析。题目对几万员工的年龄排序。故可以建立timesOfAge[oldestAge+1]的数据,里面存放每一个岁数的人员个数
6.《剑指offer》66页。旋转数组中最小的数字
key 用二分查找法可以使时间复杂度降低到log(n)
7.《剑指offer》75页斐波那契数列。定义f(n)=f(n-1)+f(n-2)。
解决问题:一只青蛙一次可以跳一级台阶同时也可以跳两级台阶。请问跳n 阶台阶共有多少种跳法。分析,在跳到n阶台阶前有两种情况,1:处在n-1阶台阶上,跳1级到达n阶台阶。2:处在n-2阶台阶上,跳2级到达n接台阶。故f(n)=f(n-1)+f(n-2)
8.《剑指offer》78页二进制数中1的个数
解法1 负数右移最高位补1,防止该现象,用flag=1左移的结果与n做按位与操作。当flag为负数时,按位与操作结束。
解法2 key 把一个整数减1,与原来的数做与运算,则能把左右边的1变为0,则一个整数的二进制表示中有多少个1,就能进行多少次这个操作。
9. 《剑指offer》82页判断一个数是不是2的整数次方。
key 2的整数次方的二进制表示只有一个1,故可以使用8中的解法2
10.两个整数m和n,计算m需要改变多少个二进制位的个数才能得到n,如10的二进制表示1010,13的二进制表示1101,则要改变3个
key 做抑或操作后,看二进制中1的个数
11《剑指offer》96 未懂
12《剑指offer》99页 已知一个单向链表的头指针和一个节点的指针,要求在O(1)的时间复杂度内删除这一个节点
key 常规方法从头遍历找到该节点前驱为O(n)。故通过给出该节点的指针找到该节点的后继节点,然后把值赋值到该节点,删除该节点后一个节点的存储空间。
13《剑指offer》102页 调整整数组顺序使奇数位于偶数的前面
key p1,p2两个指针(即数字),p1从前往后移,p2从后往前移。前者遇到偶数停下,后者遇到奇数停下。然后交换顺序。直到p1>p2。前者遇到偶数停下,后者遇到奇数停下是根据题目"使奇数位于偶数的前面"设定的。题目不同则停下条件不同。故这儿的条件判断可以写成函数形式,通过函数返回值判断
14《剑指offer》119页 未懂
15《剑指offer》127 顺时针打印矩阵
key 一圈一圈的打印,要点1:判断该圈是否要打即,(cloumns>starts*2&&rows>starts*2),其中starts初始值为0,每打印一圈,start值自增一次;要点二:每圈有四条路径,即左到右,上到下,右到左,下到上。若该圈需要打,则一定会有第一条路径,接着判断其余三条路径是否需要打印。
16《剑指offer》132 自定义栈数据结构。在该栈中能得到该栈中最小的元素min函数。在该栈中,调用min,push,pop的时间复杂度都为1
key:使用一个辅助栈,每向栈中push一次,辅助栈push入栈中当前最小的元素。栈每pop一次,辅助栈pop出栈顶的元素。这样min值就为辅助栈中的栈顶的值
17《剑指offer》134 给出一个入栈序列,判断某序列是否可能为该栈的弹出顺序。
key:元素逐一入栈,每压入一个元素,判断此时栈顶是否为即将弹出的元素,若是,则弹出该元素,继续入栈;若不是,继续入栈,若元素都入栈完毕,还不是要弹出的非弹出序列,则判断该弹出序列不可能成立
18《剑指offer》 137页。按层打印树。
key。利用队列,每打印一个结点后,再把该结点的左右儿子压入队列,然后再打印队列中的下一个元素
19《剑指offer》140页 判断一个数组,该数组是否可能是某个二叉搜索树的后序遍历序列。
key。二叉树的左子树小于根,右子树大于根,数组的最后一个元素是根。通过sequence[i]<root的条件找到左子树和右子树的分界后,在右子树的数据部分若再发现小于根的数据,则可以return false,再在分隔的左右子树数组中递归调用该函数,return left&&right;
20.《剑指offer》143页 输入一个二叉树和一个整数,打印二叉树中和为该整数的所有路径。该路径只统计从树的根节点往下一直到叶子节点的路径。
key 可以用递归思想,若当前为NULL,且当前和为0,则为有效路径。
21.《剑指offer》147页 复杂链表的复制。该链表除了有一个常规的m_pNext指针指向下一个结点外,还有一个m_pSibling指向链表中的任意结点或者NULL。请实现该复杂链表的复制。
key:由于m_pSlibing任意指向,所以若先复制m_pNext链表后再复制m_pSibling,则需要从表头定位m_pSlibing,故时间复杂度O(N^)。故正解思路如下:将复制的链表逐个插入到原结点后边,则新结点的m_pSlibing应为源节点的m_pSlibing->next。赋值好新结点的m_pSlibing后就可以重新定位p_mNext,得到新的赋值链表
22.《剑指offer》151页 输入一个二叉搜索树,将其转化为一个排序的双向链表。要求不能创建人和新的结点,只能调整数中结点指针的指向。即m_pLeft和m_pRight指向。
key:递归思想,未懂
23.《剑指offer》154页 输入一个字符串,打印该字符串的所有排列
key:把一个问题拆分为和它类似的问题后,就可以用递归的思想了。这个问题可以分为两步,首先求所有可能出现在第一个位置的字符,即把第一个字符和所有的字符交换。然后固定第一个字符,求后面所有字符的排列。显然这就是一个递归的问题。
拓展问题1:输入一个含有8个数字的数组,判断有没有可能把8个数字分别放到正方体的8个顶点上,使得正方体上三组相对的面上的4个顶点的和相等。
key。得到a1,a2,a3,a4,a5,a6,a7,a8这8个数字的所有排列,然后判断有没有一个排列符合a1+a2+a3+a4=a5+a6+a7+a8且a1+a3+a5+a7=a2+a4+a6+a8且a1+a2+a5+a6=a3+a4+a7+a8.(画一个正方体,把8个顶点用a1至a8标上,然后得到上面三组等式)
拓展问题2:在8*8的国际象棋上方8个皇后,使其不能相互攻击,即任意两个皇后不能在同一行、一列、一个对角线上。求符合条件的摆法。
key。ColumnIndex[8]中的第i个数字表示第i行的皇后所在的列好,把这8个元素用0~7初始化,即对ColumnIndex做全排列。所以对数组的两个下标i和j,判断i-j=ColumnIndex[i]-ColumnIndex[j]或者i-j=ColumnIndex[j]-ColumnIndex[i]
24.《剑指offer》163页 数组中出现次数超过一半的数字。
key1:长度过半,那么把数组排序后,若存在该数,那中间的那个数字一定是所要找的数字。step1:排序;step2:再遍历一遍数组,判断该数出现的次数。
key2:不排序,step1:遍历一次数组元素,得到可能的出现次数超过一半的数字,方法如下:当遍历到下一个数字的时候,如果下一个数字和我们之前保存的数字相同,则次数加1;若不同,则次数减1.如果次数为零,则保存下一个数字,并把次数设为1.则若存在概述,则肯定是最后一次把次数设为1的数。step2:再遍历一遍数组,判断该数出现的次数。
25.《剑指offer》167页:输入n个整数,找出其中最小的k个数
key1:若能修改数组中数的排序,则使用partition函数来解决问题。把比K小的数放在K的左边,比K大的数放在K的右边,位于数组左边的k个数就是最小的K个数,注意这K个数不一定是排序了的。该方法会使输入的数组中的数改变顺序
key2:若要求不能修改数组中的数,则顺序遍历一次数组,把数组中读到的最小的k个数放在一个容器中。容器未满k个数时,将读到的数直接加入,满了,则比较容器中最大的数和正在遍历的数。当容器满了需要1.在k个数中找最大的数。2.可能删除该数。3.可能插入新的数字。因此对于二叉树实现这个容器,能在O(logk)实现三个操作,若n个输入数字,总效率为O(n*logk)
26.《剑指offer》170页:连续子数组的最大和。要求时间复杂度为O(n)
保存两个变量,nCurSum和nGreatestSum,若nCurSum小于0了,则其对整体和的增大不可能再有贡献。nCurSum赋值为下一个读入的数,并比较if(nCurSum>nGreatestSum) nGreatestSum = nCurSum;
27.《剑指offer》174页:从1到n出现1的次数。输入一个整数n,求1到n这n个整数的十进制表示中1出现的次数,如输入12,从1到12有1,10,11,12,共出现5次
未懂
28.《剑指offer》177页:把数组排成最小的数。输入一个正整数,把数组中所有的数字拼接起来,并打印所有数字钟最小的一个。如{3,32,321}则打印321323.
key:若求出所有可能的排列,具排列组合,则有n!种排列方法,过于复杂。故考虑另外的方法。给出数字m,n要将mn和nm比较大小。直接的数学方法要考虑拼接了m和n后的溢出问题。故考虑常规的大数问题解决方法:将数字转换成字符串。然后用qsort函数解决,自定义compare函数。
29.《剑指offer》182页:丑数。把只包含银子2,3,5的数称为丑数。从按小到大1500个丑数。如6、8是丑数,但14不是丑数。习惯上把1当成第一个丑数。
key1:从1到x,每个数字都判断是否为丑数,直到判断到第1500个。丑数判断:
while(number%2==0)number/=2;
while(number%3==0)number/=3;
while(number%5==0)number/=5;
return (number==1)?true:false;
key2:基于已经找到的丑数基础上进行乘2、3、5的操作。找到以下丑数。
30.《剑指offer》186页:第一个只出现一次的字符:在字符串中找出第一个只出现一次的字符。如出入“abaccdeff”,则输出'b'.
key1:由于字母只有26,故可以利用哈希表的键值(key)是字符,而值(value)是该字符出现的次数。然后再扫描一次字符串,输出值第一次为1的字母。
31.《剑指offer》189页:数组中的逆序对。在数组中的两个数字,如果前面一个数字大于后面一个数字,则这两个数字组成一个逆序对。输出所有逆序对。
没细看
32.《剑指offer》193页:求两个链表的第一个公共结点。
key1:因为链表的元素只有一个next,故一旦公共结点了,则后面所有的结点都是公共结点。可以遍历两个链表,把两个链表中的元素的地址压入两个不同的栈,然后再从栈中弹出元素。直到找到最后一个地址相同的元素。
key2:先遍历得到两个链表长度;长的链表先走几部;一起走,直到找到相同点。
33.《剑指offer》207页:判断二叉树是否是平衡二叉树。
key1 常规递归遍历方法,二叉树中许多结点多要反复查找
34.《剑指offer》211页:数组中只出现一次的数字。一个整形数组除了两个数字之外,其他的数字都出现了两次。请写程序找到这两个数字
key1.若除了一个数字外,其他数字都出现了两次。则可以异或,最后的结果就是要找的数字
15 《剑指offer》 237页 写一个函数,求两个整数的和,函数体内不得使用+、-、*、/ 四则运算符号。
key 先相加,后进位。相加相当于位运算的异或。进位相当于位运算中的与。只有当与结果等于0才能停止
16 《剑指offer》239页 用c++设计一个不能被继承的类
key: